Question 948009: I was working on this, and have an idea of how to figure it out, but don't really understand it that well. If you could please explain how to figure this word problem out, that would be amazing!! Thank you so much!
A family has two cars. The first car has a fuel efficiency of 35 miles per gallon of gas and the second has a fuel efficiency of 40 miles per gallon of gas. During one particular week, the two cars went a combined total of 1850 miles, for a total gas consumption of 50 gallons. How many gallons were consumed by each of the two cars that week?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a uniform rates problem, all of them using the same idea:
 ; ;
You may think using variables generally like R*V=D fuel efficiency rate, volume of fuel, distance. Your example would have rate units MILES per GALLON, and obviously volume units as GALLONS, distance units as MILES.
___________________fuel effic__________volume___________distance
FIRSTCAR___________35__________________(____)___________(____)
SECNDCAR___________40__________________(____)___________(____)
TOTALS__________________________________50______________1850
There are a couple or more ways to handle the rest of the analysis. I suggest, use two variables. You want to fill-in the volume and distance slots for the two cars. I will use variables for VOLUME, m and n, respectively for first car and second car.
___________________fuel effic__________volume___________distance
FIRSTCAR___________35__________________(m)______________(35m)
SECNDCAR___________40__________________(n)______________(40n)
TOTALS__________________________________50______________1850
Use the columns for total values to form two linear equations in the variables m and n. I am choosing variables for the volumes mostly because the question ASKS FOR FINDING THOSE VOLUMES.

Solve this system for m and n.
--
Note that you might want to choose variables as 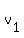 and and 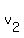 , the subscripts corresponding to first and second car. This variable labeling would be better in this example, but I simply chose m and n so as to avoid the extra text for forming subscripts, and that maybe on the algebra.com system, single variables are easier to read than subscripted ones. Typing would be v[1] and v[2], so not as fast to type. , the subscripts corresponding to first and second car. This variable labeling would be better in this example, but I simply chose m and n so as to avoid the extra text for forming subscripts, and that maybe on the algebra.com system, single variables are easier to read than subscripted ones. Typing would be v[1] and v[2], so not as fast to type.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I was working on this, and have an idea of how to figure it out, but don't really understand it that well. If you could please explain how to figure this word problem out, that would be amazing!! Thank you so much!
A family has two cars. The first car has a fuel efficiency of 35 miles per gallon of gas and the second has a fuel efficiency of 40 miles per gallon of gas. During one particular week, the two cars went a combined total of 1850 miles, for a total gas consumption of 50 gallons. How many gallons were consumed by each of the two cars that week?
Let less efficient cars (35 mpg) gas consumption, be L, and more efficient cars (40 mpg) gas consumption, M
Then 35L + 40M = 1,850_________5(7L + 8M) = 5(370)________7L + 8M = 370 ------- eq (i)
Also, L + M = 50_____M = 50 L eq (ii)
7L + 8(50 L) = 370 -------- Substituting 50 L for M in eq (i)
7L + 400 8L = 370
7L 8L = 370 400
L = 30
L, or less efficient cars gas consumption = 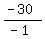 , or , or  gallons gallons
M = 50 30 ---------- Substituting 30 for L in eq (ii)
M, or more efficient cars gas consumption =  gallons gallons
You can do the check!!
===================
Send comments, thank-yous, and inquiries to D at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|