|
Question 94795: x+y=11 Use Cramer's rule to solve the x-y=5 following system of equations. If D=0, use another method to solve the system.
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x+y=11 Use Cramer's rule to solve the x-y=5 following system of equations. If D=0, use another method to solve the system.
>
To solve the system of equations by Cramer's rule:

 D is the matrix of coefficients as they appear
on the left of the equal sign:
D =
D is the matrix of coefficients as they appear
on the left of the equal sign:
D = 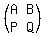 = = 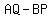 Dx is the matrix which is like D except that,
since x is the FIRST unknown letter, it has
its FIRST column
Dx is the matrix which is like D except that,
since x is the FIRST unknown letter, it has
its FIRST column 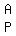 replaced
by the column of numbers on the right side of
the equal signs in the original system, replaced
by the column of numbers on the right side of
the equal signs in the original system, 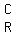 .
So
Dx = .
So
Dx =  = =  ==================================================================
Dy is the matrix which is like D except that,
since y is the SECOND unknown letter, it has
its SECOND column
==================================================================
Dy is the matrix which is like D except that,
since y is the SECOND unknown letter, it has
its SECOND column  replaced
by the column of numbers on the right side of
the equal signs in the original system, replaced
by the column of numbers on the right side of
the equal signs in the original system, 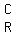 .
So
Dy = .
So
Dy = 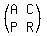 = =  =============================================================
Then x =
=============================================================
Then x =  and y = and y =  =============================================================
So for your system:
x + y = 11
x - y = 5
Write that as
=============================================================
So for your system:
x + y = 11
x - y = 5
Write that as

 D is the matrix of coefficients as they appear
on the left of the equal sign:
D =
D is the matrix of coefficients as they appear
on the left of the equal sign:
D = 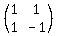 = = 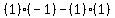 = =  = =  ==================================================
Dx is the matrix which is like D except that,
since x is the FIRST unknown letter, it has
its FIRST column
==================================================
Dx is the matrix which is like D except that,
since x is the FIRST unknown letter, it has
its FIRST column 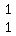 replaced
by the column of numbers on the right side of
the equal signs in the original system, replaced
by the column of numbers on the right side of
the equal signs in the original system, 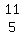 .
So
Dx = .
So
Dx = 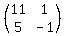 = = 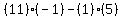 = =  = =  ==================================================
Dy is the matrix which is like D except that,
since y is the SECOND unknown letter, it has
its SECOND column
==================================================
Dy is the matrix which is like D except that,
since y is the SECOND unknown letter, it has
its SECOND column 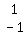 replaced
by the column of numbers on the right side of
the equal signs in the original system, replaced
by the column of numbers on the right side of
the equal signs in the original system, 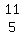 .
So
Dy = .
So
Dy = 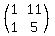 = = 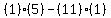 = =  = =  ====================================================
Then x =
====================================================
Then x =  = = 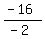 = =  and y = and y =  = =  = =  .
====================================================
Edwin .
====================================================
Edwin
|
|
|
| |