Question 947657: Someone please help me with this.
Determine the values of the variable for which the expression is defined as a real number. (Enter your answer using interval notation.)
sqrt7x^2 − 58x + 16
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If you mean 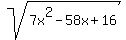 =sqrt(7x^2-58x+16), =sqrt(7x^2-58x+16),
you were missing some crucial parentheses.
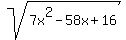 is a real number when is a real number when  . .
Otherwise, for example for  , ,
what's inside the square root is negative,
and the square root is not defined as a real number.
 is a quadratic function that graphs as a parabola. is a quadratic function that graphs as a parabola.
You can try to find its zeros by using the quadratic formula.
It does have zeros, and they are rational numbers,
so factoring also works in this case.
 is zero at is zero at  and at and at  . .
In between those numbers, 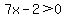 and and 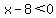 , ,
so their product,  , is negative, , is negative,
and 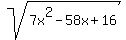 is not defined as a real number. is not defined as a real number.
For any other value of  , ,
 , ,
and 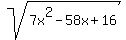 is defined as a real number. is defined as a real number.
So the answer is     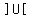     . .
|
|
|