Question 94754: Factor the polynomial completely.
I have factored other polynomials, but this one confuses me. The equation is...
-3s^2-10s+8
Thank you very much for your time!
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given:
.
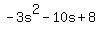
.
To factor this, you make things a little easier by factoring out -1. If you do this the
result is:
.

.
Let's not forget the -1 factor, but let's now concentrate on factoring the polynomial 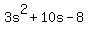 . .
.
Since the 3 preceding the s-squared term can only be factored into 3 and 1 we know if the
polynomial can be factored, the factors must be of the form:
.
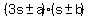
.
where "a" and "b" must be a factor pair of 8 ... in other words "a" and "b" must be either
4 and 2 or 8 and 1. And, considering the signs of "a" and "b", the terms must multiply with
3 and 1 to result in the middle value + 10. After some thought, you might see that if
"b" were +4 and "a" were -2, the factors would become:
.
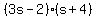
.
The cross product of +4 times +3s is +12s. And the cross product of -2 and s is -2s. These
cross products combine to give +12s - 2s = +10s which is the middle term of the polynomial
being factored.
.
But don't forget that we originally factored a -1 from the polynomial. Therefore, when
we put that factor into the solution the answer becomes:
.
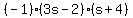
.
and by convention, the "1" is understood so the answer is just:
.
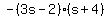
.
This is the answer. You could also move the minus sign into one set of parentheses.
For example, you could have the answer in the form:
.
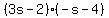
.
and if you multiply this out you will get back to the original polynomial you were given
to factor.
.
Hope that this helps you to understand the way to get to an answer for this problem.
.
|
|
|