Question 946768: A shopkeeper wants to mix three types of nut to produce a special nut mix. She will
mix peanuts, brazil nuts and cashew nuts. The brazil nuts sell for £1.10 per 100g, and
as she has only 20 kg left, she wants to use all of them. The peanuts sell for £0.50 per
100g and the cashews for £0.90 per 100g, and there are plenty of peanuts and
cashews. How much of each should be in the mixture if the shopkeeper will be
producing 100 kg of mixed nuts to be sold at £0.80 per 100g?
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! p, b, c, for peanut, brazil nut, cashew nut quantities IN KILOGRAMS.
NUT_________|_______PRICE
peanut______|_______0.5 per 0.1 kg
brazil______|_______1.10 per 0.1 kg
cashw_______|_______0.90 per 0.1 kg
Already known to use b=20 kg, ALL of the brazil nuts for the mixture.
WANT: 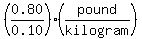 mixture price. Also mixture quantity 100 kg.
Account for mass or kilograms and account for total cost, and compare to the required price.
 AND  .
Those are a system of, once simplified, two linear equations in the two unknown variables, p and c.
The price equation initially simplifies to  .
Go on from there....
Understand, "pound" as used here is a MONEY unit.
|
|
|
