Question 946081: financial planning a stockbroker has $200,000 to invest in stocks and bonds. she wants to invest at least $100,000 in stocks And at least $50,000 in bonds. If stocks have an annual yield of 9% and bonds have an annual yield of 7%, how much should she invest in each to maximize her income. Fing the maximum return.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x = amount invested in stocks.
let y = amount invested in bonds.
she has up to 200,000 to invest in stocks and bonds.
equation for that is x + y <= 200,000
solve for y to get y <= 200,000 - x
she wants to invest at least 100,000 in stocks.
equation for that is x >= 100,000
she wants to invest at least 50,000 in bonds.
equation for that is y >= 50,000
stocks earn her 9% per year.
bonds earn her 7% per year.
she wants to maximize her revenue.
revenue becomes her objective function.
if we let z represent the objective function, then the equation for that is z = .09x + .07y
her objective function is z = .09x + .07y
her constraints are:
x >= 100,000
y >= 50,000
y <= 200,000 - x
since these are 2 dimensional equations, they can be graphed on the two dimensional graphing plane where x is the horizontal axis and y is the vertical axis.
the equality portion of the constraint equations are graphed.
the inequality portion of the constraint equations determine the feasible region.
the maximum / minimum solution is at the corner points of the boundaries of the feasible region.
the graph is shown below:
look below the graph for further comments.
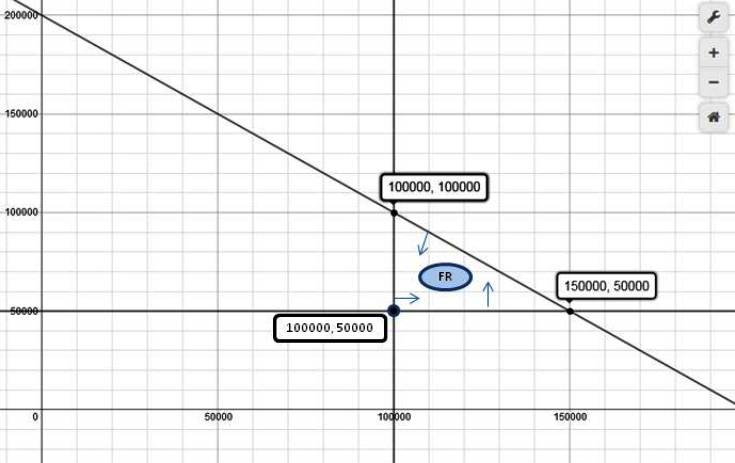
The feasible region is shown as FR.
it is below the line of y = 200,000 - x
it is above the line of y = 50,000
it is to the right of the line of x = 100,000
the feasible region corresponds to the inequality portion of:
y <= 200,000 - x
y >= 50,000
x >= 100,000
since the solution can be on the lines as well as the area bounded by the lines, then the lines are shown as solid lines.
the corner points of this feasible region are where the maximum or minimum solutions lie.
when x = 100,000 and y = 50,000, the objective function is .09 * 100,000 + .07 * 50,000 which is equal to 12,500.
when x = 100,000 and y = 100,000, the objective function is .09 * 100,000 + .07 * 100,000 which is equal to 16,000.
when x = 150,000 and y = 50,000, the objective function is .09 * 150,000 + .07 * 50,000 which is equal to 17,000.
maximum revenue is attained when 150,000 is invested in stocks at 9% and 50,000 is invested in bonds at 7%.
|
|
|