Question 945995: given two sides of a triangle 5 and 10, find the following,
range of possible side lengths for triangle to be acute
to be right
to be obtus
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = length of the third side. = length of the third side.
To be a triangle, it must be
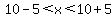 ---> ---> 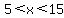
Within that range,
very short and very long third sides yield  triangles; triangles;
there are  values that yield right triangle, amd values that yield right triangle, amd
in between those values we get acute triangles:

 or or 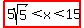 --> obtuse triangle --> obtuse triangle
 or or  --> right triangle --> right triangle
 --> acute triangle --> acute triangle
For  , we have an isosceles triangle, , we have an isosceles triangle,
with the vertex angle being the smallest angle, with measure  , ,
because it is opposite the shortest side.
The other two angles are the base angles,
each measuring  , ,
so they are acute too, and we have an acute triangle.
For The  values that yield right triangles, we use the Pythagorean theorem. values that yield right triangles, we use the Pythagorean theorem.
For 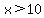 : :
We would get a right triangle with  and and  legs if and only if legs if and only if
 ) )
 --> -->
If  is the longest side length, is the longest side length, 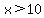 , ,
the largest angle would be opposite that longest side.
That angle would be greater than a right angle (an obtuse angle),
if and only if  . .
So, we would get an obtuse triangle if and only if 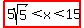 . .
Also with  being the longest side length, being the longest side length, 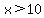 , ,
the largest angle, opposite that side, would be less than a right angle (acute) if and only if 
So, we would get an acute triangle if 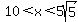 , ,
For 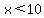 : :
We would get a right triangle with  leg and leg and  hypotenuse if and only if hypotenuse if and only if
 ---> --->
 ---> ---> . .
When the longest side is the one with length 10,
the angle opposite that side is the greatest angle.
If  , ,
we would have 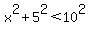 : :
the greatest angle would be obtuse and the triangle would be obtuse.
If 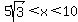 , ,
we would have 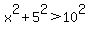 : :
the greatest angle would be acute and the triangle would be acute.
|
|
|