Question 945137: an equilateral triangle is drawn by joining the midpoints of the sides of another equilateral triangle. a third equilateral triangle is drawn inside the second one joining the midpoints of the sides of the second equilateral triangle, and the process is continued indefinitely. find the sum of all perimeters of all equilateral triangles, if the side of the largest equilateral triangle is 24?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the side of the first/largest equilateral triangle is 24,
its perimeter is  . .
Joining the midpoints of the sides of an equilateral triangle
 splits that triangle into splits that triangle into
4 equilateral triangles whose sides are half as long as the sides of the original equilateral triangle.
Consequently, the perimeter of the second triangle will be half the perimeter of the first.
So, the sum of all the infinite perimeters is
 . .
The sum 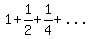 is the sum of an infinite geometric sequence, is the sum of an infinite geometric sequence,
with first term  and common ratio and common ratio  . .
It is easy to see that it adds up to  , because , because
when you added  more term to the first term, you were more term to the first term, you were  short of short of  ; ;
when you added to that term number  terms you were terms you were  short of short of  , ,
and you keep being 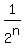 short of short of  as as  keeps increasing. keeps increasing.
If you (or your teacher) insist on using formulas,
the sum of the first  terms of geometric progression (if such a sum exists) is terms of geometric progression (if such a sum exists) is
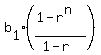 , and with , and with  , ,
the sum of the infinite terms of geometric progression is
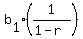 . .
In this case 
|
|
|