SOLUTION: Find the equation of the circle with center on the line X-5y+9=0, tangent to X-3y-11=0, and has radius √10

It appears that there are two solutions:



Let the center of the circle be (h,k).

Then the perpendicular distance from the center of the circle
to the line to which it is tangent must equal to the radius of the circle.

That's the green lines.


The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is
d = 


Therefore, the perpendicular distance from ine point (h,k) to the line 

      x-3y-11 = 0 
is




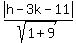
It must equal to the radius  so


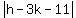Since (h,k) is on the line x-5y+9=0
x-5y+9=0
h-5k+9=0
h=5k-9
Substitute in




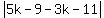
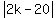That breaks into two equations:

2k - 20 = 10     and    -(2k - 20) = 10
     2k = 30     and      -2k + 20 = 10
      k = 15     and           -2k = -10
                                 k = 5

  h = 5k - 9                h = 5k - 9
  h = 5(15) - 9             h = 5(5) - 9
  h = 75 - 9                h = 25 - 9
  h = 66                    h = 16

(h,k) = (66,15)             (h,k) = (16,5)

The equation of any circle is

(x-h)² + (y-k)² = r²

The radius r is given as , so r² = 10  

So the two circles' equations are:

(x-66)² + (y-16)² = 10   and  (x-16)² + (y-5)² = 10

Edwin