Question 944241: Which set of line segments could create a right triangle?
15, 30, 35
15, 36, 39
15, 20, 29
5, 15, 30
Found 2 solutions by Edwin McCravy, MathTherapy:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
15, 30, 35
Try the Pythagorean theorem:
a² + b² = c²
15² + 30² = 35²
225 + 900 = 1225
1125 = 1225
That's false, so 15, 30, 35 cannot be used to create a right triangle,
because the Pythagorean theorem does not give equality.
-----------------------------------------
15, 36, 39
Try the Pythagorean theorem:
a² + b² = c²
15² + 36² = 39²
225 + 1296 = 1521
1521 = 1521
That's true, so 15, 36, 39 can be used to create a right triangle,
because the Pythagorean theorem gives equality.
---------------------------------------------------
15, 20, 29
Try the Pythagorean theorem:
a² + b² = c²
15² + 20² = 29²
225 + 400 = 841
625 = 841
That's false, so 15, 20, 29 cannot be used to create a right triangle,
because the Pythagorean theorem does not give equality.
--------------------------------------------------------
5, 15, 30
No use to try the Pythagorean theorem on this because, to even have any
triangle at all, the sum of the two shorter sides MUST be GREATER THAN the
longest side, and 5+15 is only 20, which is not greater than what would
have to be the longest side, namely 30.
-------------------------------------------------------
Answer: 15, 20, 29
Edwin
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Which set of line segments could create a right triangle?
15, 30, 35
15, 36, 39
15, 20, 29
5, 15, 30
 as as 
Notice also that if 15, 36, and 39 are divided by 3, we get: 5, 12, and 13.
This is actually one of the pythagorean triples: 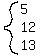
|
|
|