The other tutor's answer above is incorrect. The other tutor gave the
solution for  . The 2 and the 16 are not in
parentheses so they are not raised to those negative powers. Only x is
raised to those negative powers in your equation.
-----------------------------------------------------------
. The 2 and the 16 are not in
parentheses so they are not raised to those negative powers. Only x is
raised to those negative powers in your equation.
-----------------------------------------------------------
 Divide both sides by 2
Divide both sides by 2
 Write the factors with negative exponents as denominator
factors with positive exponents:
Write the factors with negative exponents as denominator
factors with positive exponents:
 Cross-multiply:
Cross-multiply:
 Get 0 on the right sides:
Get 0 on the right sides:
 Factor out x³
Factor out x³

 ,
, 
 ,
,  0 is not a solution because 0 may only be raised to
positive powers, and the original has negative powers.
The second equation requires the factorization of the
difference of two cubes:
0 is not a solution because 0 may only be raised to
positive powers, and the original has negative powers.
The second equation requires the factorization of the
difference of two cubes:
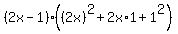













 So there are three solutions
So there are three solutions  ,
, 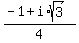 ,
,  Edwin
Edwin