|
Question 943929: I am confused on how hyperbolas open left or right, can you please explain that to me. and I have to solve these and not sure if left or right
1. 8x^2 - 10y^2 - 48x - 100y - 98 = 0
Found 2 solutions by MathLover1, KMST:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hyperbolas consist of two vaguely parabola shaped pieces that open either up and down or right and left. Also, just like parabolas each of the pieces has a vertex. Note that they aren’t really parabolas, they just resemble parabolas.
There are also two lines on each graph. These lines are called asymptotes and as the graphs show as we make  large (in both the positive and negative sense) the graph of the hyperbola gets closer and closer to the asymptotes. large (in both the positive and negative sense) the graph of the hyperbola gets closer and closer to the asymptotes.
The asymptotes are not officially part of the graph of the hyperbola. However, they are usually included so that we can make sure and get the sketch correct. The point where the two asymptotes cross is called the 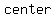 of the hyperbola. of the hyperbola.
There are two  forms of the hyperbola: forms of the hyperbola:
form:  => hyperbola opens left and right,has vertices at ( => hyperbola opens left and right,has vertices at (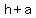 , , ) and ( ) and (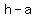 , , ) , ) ,
and form  =>hyperbola opens up and down, has vertices ( =>hyperbola opens up and down, has vertices ( , ,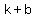 ) and ( ) and ( , ,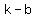 ) )
both have:
Center at ( , , ), Slope of Asymptotes ± ), Slope of Asymptotes ±  , Equations of Asymptotes , Equations of Asymptotes  = =  ± ±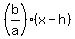
1.
 first write it in standard form first write it in standard form
 ...complete square ...complete square









as you can see, you have hyperbola in a form:
 => Opens up and down, => Opens up and down,
 , ,  , => center at ( , => center at ( , , ) )
 , ,  , ,
vertices ( , ,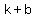 ) =( ) =( , ,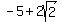 ) and ( ) and ( , ,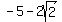 ) )

Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Parabolas are single curves that can open up or down.
There is no "or" with hyperbolas;
a hyperbola can open up AND down,
or it could open left AND right,
or it could open southeast and northwest,
or .....
Hyperbolas, like most people, have 2 arms (two separate curves, or "branches").
Those arms are flirty curves that approach the center,
only to turn around before getting to that center,
and then go away along a symmetric path.
A popular kind of hyperbola opens to the left and right,
and (with its center) looks like parentheses drawn the wrong way around a dot/point:
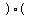
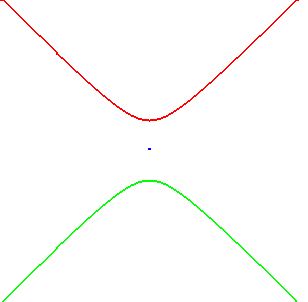
Another popular shape is with the openings towards top and bottom:
 . .
There are tilted hyperbolas too, like
 , but those make calculations too complicated, , but those make calculations too complicated,
so you will (hopefully) not see that.
The curve represented by your equation is a hyperbola.
We know that because the terms in  and and  have coefficients (8 and -10) with opposite signs. have coefficients (8 and -10) with opposite signs.
You may be able to figure out which ways the hyperbola opens through some formula given in class,
but I have to work up what that hyperbola looks like to understand it.
(Besides, I cannot memorize formulas, so I resort to understanding and thinking through the problem).
To figure out what your hyperbola looks like, you can "complete the squares":


Now I am going to add some terms to both sides of the equal sign to get an equivalent equation

There is a method to mu madnes, as you will soon see:


Do you see what I meant by "completing the squares"?
I was building up 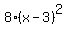 from from 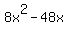 by adding by adding  , ,
and I was building up 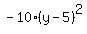 from from 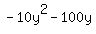 by adding by adding 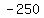 . .
From  , ,
I divide both sides of the equal sign by 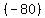 to get a to get a  on the right side: on the right side:


We can rearrange the equation to
 if we want. if we want.
The last equation looks more like the textbook
 for a hyperbola opening up and down. for a hyperbola opening up and down.
(I just checked).
Without studying the book, you can realize that the curve represented by the equation

1) is symmetrical with respect to the lines
 <---> <---> and and
 <---> <---> , ,
because that equation does not distinguish between  and and  , ,
or between  and and  , ,
or between  and and  , ,
or between  and and  ; ;
2) you also realize that as  <---> <---> <---> <--->
 <---> <---> <---> <---> . .
So the hyperbola opens up and down,
with no points between  and and 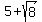 . .
-
|
|
|
| |