|
Question 943382: the coordinates of vertices X and Y of an equilateral XYZ are (-4,0) and (4,0), respectively. the coordinates of Z may be what?
I would like step-by-step process how you did this problem. thank you very much.
Answer by reviewermath(1029)   (Show Source): (Show Source):
You can put this solution on YOUR website! The coordinates of vertices X and Y of an equilateral XYZ are (-4,0) and (4,0), respectively. the coordinates of Z may be what?
Solution:
The slope of the line containing the segment XZ is equal to [tan (60 degrees)] =  . The x-intercept is -4, so the equation of the line XZ is . The x-intercept is -4, so the equation of the line XZ is
y =  x + x + 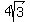 . .
The slope of the line containing YZ is numerically equal to the slope of XZ but opposite in sign. The x-intercept is 4, so the equation of the line YZ is
y =  x + x + 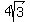 . .
To get the coordinates of Z, we solve for the intersection of the lines XZ and YZ.
 x + x + 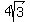 = =  x + x + 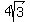
 x = 0 x = 0
x = 0
Therefore, y =  (0) + (0) + 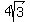 = = 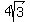
The coordinates of Z are (0, 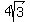 ) [Answer] ) [Answer]
By symmetry, the other possible answer is (0, 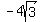 ) )
|
|
|
| |