Question 942092: I can't seem to find the next number in this sequence;
6, 3, -4, -14, -26, -39, -52
Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39623)   (Show Source):
You can put this solution on YOUR website! 6 to 3, subtracted 3;
3 to -4, subtracted 7;
-4 to -14, subtracted 10;
-14 to -26, subtracted 12;
-26 to -39, subtracted 13;
-39 to -52, subtracted 13...
AT that step, the pattern seems to be breaking. Does the difference now go in the other direction or stay at 13?
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! If a general formula is to be a polynomial,
you can find it by calculating differences between consecutive terms,
and then differences between the already found differences.
The second term is  more than the one before (the first term).
THat means to get to the second term you add  to the term before.
The third term is  more than the one before (the second term).
The next difference is  .
The next difference is  .
The next difference is  .
The next difference is  .
The differences form the sequence
,  ,  ,  , .
Their differences are
 , ,  ,  , and  :
If we calculate the differences of differences of differences,
we find that the result is always the same.
The differences of differences increase by 1 each time.
The next difference of differences should be  :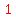 
That means the next difference should be
 : 
and that would make the next number
 : 
|
|
|
