|
Question 94085This question is from textbook Algebra 2
: Use intercepts to graph each equation.
5x - 8y = 16
This question is from textbook Algebra 2
Found 2 solutions by bucky, jim_thompson5910:
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! You are given the equation:
.
.
and are told to use intercepts to graph the equation.
.
The intercepts of a linear equation are the coordinate points where it crosses the y-axis and
where it crosses the x-axis. If you plot these two points, you can get the graph by using a
straight edge to draw a line that extends through these two points and beyond.
.
The coordinate point on the y-axis will have an x-value of what? When you think about it,
you can see that any point on the y-axis will have an x-value of zero. So to get the y-value
from this equation, you can set x equal to zero and solve for y. When you do set the value
of x equal to zero, the equation reduces to:
.
.
and the 5*0 term is equal to zero so it drops out and the equation is down to:
.
.
Now you can solve for y by dividing both sides of the equation by -8 to get:
.
.
We now know that the graph crosses the y-axis at the point (0, -2).
.
Again you have to think about the point where the graph crosses the x-axis. Any point on the
x-axis will have a y-value of zero. Therefore, in the given equation if we set y equal to zero
the value of x that we get identifies the point where the graph crosses the x-axis.
.
So set y equal to zero and the equation becomes:
.
.
The -8*0 term multiplies out to zero and, therefore, drops from the equation, leaving just
the equation:
.
.
You can now solve for x by dividing both sides by 5 to get:
.
.
So the x-intercept point is at (16/5, 0}
.
Plot this point along with the previous y-intercept point of (0, -2) and you have two points
that you can use to draw the graph.
.
When you get done your graph should look like this:
.
.
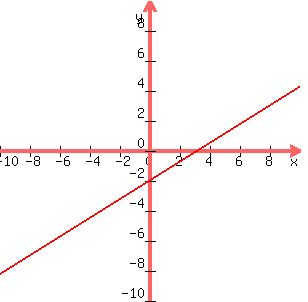
Hope this helps you to see your way through the problem.
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
 Start with the given equation
Let's find the x-intercept
To find the x-intercept, let y=0 and solve for x:
 Plug in 
 Simplify
 Divide both sides by 5
So the x-intercept is ( ,0) (note: the x-intercept will always have a y-coordinate equal to zero)
------------------
Start with the given equation
Now let's find the x-intercept
To find the y-intercept, let x=0 and solve for y:
 Plug in 
 Simplify
 Divide both sides by -8
 Reduce
So the y-intercept is (0, ) (note: the y-intercept will always have a x-coordinate equal to zero)
------------------------------------------
So we have these intercepts:
x-intercept: (,0)
y-intercept: (0,)
Now plot the two points (,0) (which is the point (3.2 ,0) in decimal form) and (0,)
Now draw a line through the two points to graph
 graph of through the points (,0) and (0,)
|
|
|
| |
