Question 940706: Where does the line (x; y; z) = (4; 2; 1) + t(-2;-1; 0), (t is an element of the Real numbers), intersect the plane with general
equation 2x - y + 3z = 6?
any help would be appreciated cheers
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! So the line is then,
( , ,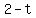 , ,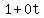 )=( )=( , ,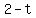 , , ) )
Substitute this into the plane equation and solve for  . .






So then,
(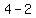 , ,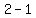 , , )=( )=( , , , , ) is the intersection point. ) is the intersection point.
|
|
|