Question 940570: is it possible to make a regular polygon where each interior angle is exactly 9 times as large as the matching exterior angle?
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! is it possible to make a regular polygon where each interior angle is exactly 9 times as large as the matching exterior angle?
-------------
Yes.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! The exterior angle and the interior angle are supplementary,
meaning that they add up to  .
Let  be the measure of the exterior angle in degrees.
Then, 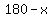 is the measure of the interior angle in degrees, and
"each interior angle is exactly 9 times as large as the matching exterior angle" translates as
 <---> <---> <---> <---> .
The exterior angle is the angle you turn around the corner/vertex, as you go around the polygon. Naturally, once you went all the way around, you have turned  , so the sum of the measures of all exterior angles is .
All the exterior angles in a regular polygon have the same measure,
so if each exterior angle measures  ,
the sum of the exterior angles in the polygon is
 <---> <---> .
It is possible to make a polygon with 20 sides angles, so the answer is  .
If we had found a result for  that was not a whole number, or was a whole number less than 3, the answer would have been no.
|
|
|
