Question 939658: I was hoping to get some help I took this problem from my book, I have homework problems that are the same can some one show me how to work this?
For each set of ordered pairs, determine if the set is a function, a one-to-one function, or neither. Reverse all the ordered pairs in each set and determine if this new set is a function, a one-to-one function, or neither.
{(1, 2), (2, 1), (3, 4), (4, 3)}
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To have a  , the pairs, of the form (x,y), , the pairs, of the form (x,y),
must be such that each x is paired with only one y.
To have a 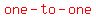  , you need pairs, of the form (x,y), , you need pairs, of the form (x,y),
That form a function (see above),
and also such that each y is paired with only one x.
If you have a 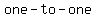  , ,
reversing the pairs you get another one-to-one function.
Also, if reversing the pairs of a function you get another function,
both functions are one-to-one functions,
and we say that each of the two functions is the 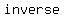 of the other function. of the other function.
That is a lot of  to remember, and I am sorry that you have to go through this. (I am also glad I don't have to remember those names any more). to remember, and I am sorry that you have to go through this. (I am also glad I don't have to remember those names any more).
Is the given set a function?
The first members of each pair form the set {1,2,3,4} .
Since the first numbers in the pairs are all different,
you do not have the same x shown twice, paired with different y's.
After you reverse all the ordered pairs, is the new set a function?
Reversing the pairs you end up with
{ (2,1) , (1,2) , (4,3) , (3,4) }.
Thee new first members of each pair form the set {2,1,4,3} .
Again, those x values are all different,
so there is no danger of having the same one paired with two different y values.
The new set is also a function.
The original set and the reversed set are both 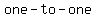 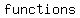 . .
MORE NAMES:
Maybe you were taught a 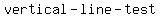 to find if a to find if a 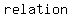 , ,
meaning a set of 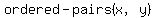 , is a function, , is a function,
and a 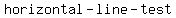 to find if it is also a to find if it is also a 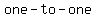  . .
Those go like this:
1) You plot your ordered pairs as points on an x-y chart.
I plotted your points (circled in green) below.

2) If there is no way to "skewer" two or more of the points with a vertical line,
your relation is a  . .
That is the 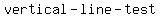 . .
3) If there is also no way to "skewer" two or more of the points with a horizontal line,
your relation is a 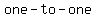  . .
That is the  . .
NOTE: I do not believe they should make you memorize all those names in math class.
You have to memorize enough stuff in the other classes, and memorizing makes math boring.
I think math is a lot of fun, and I use all the time
it to solve real life problem,
and to satisfy my curiosity about puzzling stuff that is not a problem to me
(like the problems in this website).
Unfortunately, I am not a teacher,
and they would not let me be one,
because I am not good enough at boring students to tears.
|
|
|