SOLUTION: How do I find all values between 0 and 360 for the equation cscx= -2.833. Thank you.

Click here to see ALL problems on Trigonometry-basics

Question 938714: How do I find all values between 0 and 360 for the equation cscx= -2.833. Thank you.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website!
cscx= -2.833
----
You have to use trig tables (obsolete) or technology (calculator).
----
x = arccos(-1/2.833)) = 110.67 degrees or 360-110.67 = 249.33 degrees
--------------
Cheers,
Stan H.
---------------

Answer by Edwin McCravy(20065) (Show Source):
You can put this solution on YOUR website!

The other tutor's answer is wrong. He was thinking of the secant, not the cosecant.

How do I find all values between 0 and 360 for the equation cscx= -2.833. Thank you.

We know that the cosecant is the reciprocal of the sine, and since -2.833 is negative, we know that the angle values are in the 3rd and 4th quadrants. Now we find the reference angle. Make sure the calculator is in degree mode and not radian mode. We use the absolute value 2.833, and convert this cosecant to a sine, by finding its reciprocal 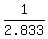or 0.352987038. Then we use the inverse sine key, sin^-1 to find the angle that has 0.352987038 for its sine. We get 20.66985951�. But now we must get the 3rd and 4th quadrant angles which have this for their reference angles. For the angle in the 3rd quadrant we add 180�+20.66985951� = 200.66985951� For the angle in the 4th quadrant we subtract 360�+20.66985951� = 339.3301405�. The quick way with a TI-84: Press 2ND Press SIN Type 2.833 Press x^-1 Press ENTER Read 20.66985951 Press STO Press the key that has "X,T,,n" on it Press ENTER type 180+ Press the key that has "X,T,"X,T,,n" on it Press ENTER Read 200.6698595 type 360- Press the key that has "X,T,qn" on it Press ENTER Read 339.3301405 Edwin