|
Question 938490: An astronaut on the moon throws a baseball upward. The astronaut is 6ft, 6 in. tall and the initial velocity of the ball is 30 ft per second. The height s of the ball in feet is given by the equation,s=-2.7t^2+30t+6.5, where t is the number of seconds after the ball is thrown.
The ball will never reach a height of 100ft. How can this be determined algebraically?
Found 3 solutions by josmiceli, ankor@dixie-net.com, nerdybill:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! An astronaut on the moon throws a baseball upward.
The astronaut is 6ft, 6 in. tall and the initial velocity of the ball is 30 ft per second.
The height s of the ball in feet is given by the equation,s=-2.7t^2+30t+6.5, where t is the number of seconds after the ball is thrown.
The ball will never reach a height of 100ft.
How can this be determined algebraically?
:
Find the axis of symmetry of the equation, then find max height
t = -b/(2a)
t = 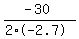
t = +5.556 sec to reach max height
Find s when this the value of t
s = -2.7(5.56^2) + 30(5.56) + 6.5
s = -2.7(30.86) + 166.65 + 6.5
s = -83.32 + 166.65 + 6.5
s ~ 90 ft is max height
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since 's' predicts the height from the equation:
s=-2.7t^2+30t+6.5
Just by looking at the above equation we determine that it is a
parabola (quadratic) (polynomial of degree 2)
that opens downwards (negative leading coefficient)
.
Therefore, the vertex will be the peak of its travel.
time t to arrive at peak is
t = -b/(2a)
t = -30/(2*(-2))
t = -30/(-4)
t = 7.5 secs
.
s = -2.7t^2+30t+6.5
s = -2.7(7.5)^2+30(7.5)+6.5
s = 79.625 feet (max height)
|
|
|
| |