An old machine requires 3 times as many hours to complete a job as a new machine. When both machines work together, they require 9 hours to complete a job. How many hours would it take the new machine to finish the job alone?
Make this chart:
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | | |
-----------------------|-------------|-----------|----------
New Machine alone | | |
-----------------------|-------------|-----------|----------
Both working together | | |
------------------------------------------------------------
How many hours would it take the new machine to finish the job alone?
Let x = the answer and put x in the middle of the last column, the
time for the new machine to finish the job alone:
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | | |
-----------------------|-------------|-----------|----------
New Machine alone | | | x
-----------------------|-------------|-----------|----------
Both working together | | |
------------------------------------------------------------
An old machine requires 3 times as many hours to complete a job as a new machine,
So put 3x in the top of the last column, or the time required for the old machine to complete the job.
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | | | 3x
-----------------------|-------------|-----------|----------
New Machine alone | | | x
-----------------------|-------------|-----------|----------
Both working together | | |
------------------------------------------------------------
When both machines work together, they require 9 hours to complete a job.
So put 9 in the bottom right corner, the time required when both machines
work together.
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | | | 3x
-----------------------|-------------|-----------|----------
New Machine alone | | | x
-----------------------|-------------|-----------|----------
Both working together | | | 9
------------------------------------------------------------
In all three cases exactly 1 job was completed, so we put 1's in all three
spaces in the first column:
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | 1 | | 3x
-----------------------|-------------|-----------|----------
New Machine alone | 1 | | x
-----------------------|-------------|-----------|----------
Both working together | 1 | | 9
------------------------------------------------------------
Now we fill in the rates in jobs per hour, That means we
divide the jobs by the hours, which is to put the number
of jobs over the number of hours:
| Number of | Rate | Time
| jobs | in | to
| completed | jobs/hr | complete
-----------------------|-------------|-----------|----------
Old Machine alone | 1 | 1/(3x) | 3x
-----------------------|-------------|-----------|----------
New Machine alone | 1 | 1/x | x
-----------------------|-------------|-----------|----------
Both working together | 1 | 1/9 | 9
------------------------------------------------------------
The equation comes from
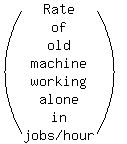
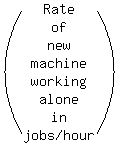
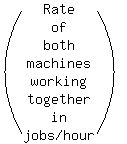
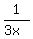
Multiply through by LCD of 9x
3 + 9 = x
12 = x
It takes the new machine 12 hours to complete the job
Edwin
