|
Question 938100: Two vertices of an equilateral triangle are (3,4)and (-2,3) the third vertex can be
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We know one side of the triangle, connecting vertices 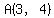 and and  . .
The length of side AB is

Side AB is a segment of a line with slope
 . .
The midpoint of AB, point P, has coordinates
 and and  . .
The equilateral triangles with side AB are ABD and ABC,
with C and D on opposite sides of segment AB.
Visualizing the location of vertices C and D is easy,
but I could not think of a simple way to calculate their coordinates.

The perpendicular bisector of AB contains the altitude of those triangles.
That perpendicular bisector is a line perpendicular to AB,
and passing through point P (the midpoint of AB).
Being perpendicular to a line with slope  , ,
that altitude is part of a line with slope  . .
 . .
Since angle PAC is a  , ,
 --> -->
So the length of PC and PD is  , ,
but what are the coordinates of C and D?
 Since the slope of CD is Since the slope of CD is  , ,  , ,
and in those two green right triangles
 ---> ---> ---> ---> ---> --->
Then,
 (rounded), (rounded),
 (rounded), (rounded),
 (rounded), and (rounded), and
 (rounded). (rounded).
|
|
|
| |