Question 937701: Which of these sequences is a geometric sequence?
1, 2, 4, 7, 11, 16, 22, …
2, 4, 8, 14, 22, 38, …
3, 6, 9, 12, 15, 18, 21, …
3, 9, 27, 81, 343, 729, …
Found 2 solutions by richard1234, MathLover1:
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3, 9, 27, 81, 243, 729, ..., (not 343)
Note: You may want to look up the definition of a "geometric sequence" as this question simply tests your understanding of the definition.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the sequence is geometric, then there is a common ratio, we must think in terms of multiplication previous term by common ratio  to get next term in sequence. to get next term in sequence.
The r-value can be calculated by dividing   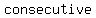 terms in a geometric sequence. terms in a geometric sequence.
The formula for calculating the Common Ratio  is: is:

1.
 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , … , …



there is no common ratio  , ,  a geometric sequence a geometric sequence
2.
 , ,  , ,  , ,  , ,  , … , …



there is no common ratio  , ,  a geometric sequence a geometric sequence
3.
 , ,  , ,  , ,  , ,  , ,  , … , …



there is no common ratio  , ,  a geometric sequence a geometric sequence
4.
9, 27, 81, 343, 729, …



 there is no common ratio there is no common ratio  , ,  a geometric sequence a geometric sequence
since you have to have one solution, I think the term 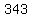 is wrong because first three terms have common ratio is wrong because first three terms have common ratio  ,if we multiply ,if we multiply 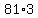 we got we got  and and 
and next one will be 
there is common ratio  , means the sequence , means the sequence  , ,  , , 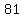 , ,  , , 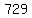 , … , … 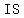 a geometric sequence a geometric sequence
|
|
|