|
Question 9377: My friend and I think that the answer to this problem is wrong and we would like a second opinion. There are actually two problems, but I will post it on another seperate page. Its and elipse problem. It reads -
Graph the ellipse and find the foci. Here is the equation - (9x^2)+(4y^2)= 9
Our disagreement is over the coordinates in which the foci are located?
Could you please help us?
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! 
Divide both sides by 9:
Rewrite this as:
The center of the ellipse is at (0,0), and the radius in the x direction is 1, the radius in the y direction is  . Therefore the major axis is in the Y-direction, and the foci will be on the y-axis at (0, c) and (0, -c), where 
Solve for c:
 or 
Therefore, I have the foci at 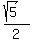( 0,  ) and ( 0, ).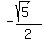
R^2 at SCC
|
|
|
| |
