Question 936217: A store has a rectangular parking lot that is 15 feet longer then it is wide. The owner wants to put a
4-foot-wide sidewalk along the outside of the parking lot. If the total surface area of the sidewalk and the parking lot together is 46,384 square feet. What is the width of the parking lot, not including the sidewalk?
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! You should draw a picture of the description.
Assign some variables:
w, width of the parking lot
L, length of the parking lot
u, the uniform width of sidewalk
T, total area of parking lot and sidewalk;
L=w+15, and if wanted, a variable could be assigned for "15".
Unknown variables are w and L.
You are also given:
u=4;
T=46384.
Setup some expressions and equations.
Lot area, wL, or 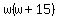 . .
'



Check the composition of that equation carefully. The ONLY unknown is w, and this, parking lot width, is what the question is to be answered. All the other variables are KNOWN. You have a choice of solving for w completely symbolically, or substituting the known values now and simplifying, and then solving for w. Substituting for u and T now and simplifying would probably be more comfortable.
....otherwise, you can go ahead with

and try to simplify it....
|
|
|