Question 935794: Let f(x)=2x^2+7x-4/x^3-1
A. What is the domain of f(x)?
B.What is the range of f(x)?
C.What are the roots of f(x)?
D.determine the end behavior of f(x)?
E.Where will f(x) intersect the y-axis?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You wrote 2x^2+7x-4/x^3-1 =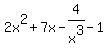 , ,
but I suspect that you meant f(x)=(2x^2+7x-4)/(x^3-1)=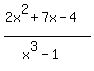 . .
If  , ,
A. the domain of  is all the values of is all the values of  that give a value to that give a value to  . .
That means all the values of  that that
make 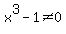 , and that is all the values of , and that is all the values of  such that such that
 , ,
because  ---> ---> ---> ---> . .
Other that for  , ,  is a continuous function, so it varies continuously. is a continuous function, so it varies continuously.
It is zero and it changes sign at the points where  . .
It has no absolute maximum or minimum, because
as  approaches approaches  , ,
the numerator approaches  , ,
while the denominator approaches  , ,
which makes the absolute value of  to increase without bounds. to increase without bounds.
At  the denominator changes sign, the denominator changes sign,
with  <---> <---> and and 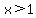 <---> <--->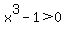 , ,
so  ---> --->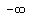 as as  approaches approaches  from the left, and from the left, and  ---> ---> as as  approaches approaches  from the right. from the right.
B. The range of  is all the values is all the values  can take. can take.
That is all real numbers or 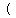 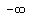   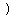 . .
Graphing the function would show you that,
but I am not sure how you are expected to demonstrate that.
One way would be to demonstrate that
 <---> <---> <---> <---> has a solution for every possible real value of has a solution for every possible real value of  . .
It is obvious that it is so,
because  is an odd-degree polynomial, is an odd-degree polynomial,
an those always hit zero somewhere.
C. The roots of  are the roots of are the roots of  , ,
and we find them by solving  . .
Factoring we get
 --> --> --> --> --> --> . .
So, the roots are  and and  . .
D. The end behavior of  is given by is given by
 . .
The limit is so because rational functions tend to zero at the ends
when the degree of the denominator (3 in this case)
is greater than the degree of the denominator (2 in this case).
So,  (the x- axis) is the horizontal asymptote. (the x- axis) is the horizontal asymptote.
The function is positive for  , ,
so it approaches the positive x-axis from above.
At the other end, where 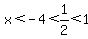 , ,
 approaches the negative x-axis from below. approaches the negative x-axis from below.
E.Since the y-axis is the line  , ,
f(x) intersect the y-axis at the point with  , (0,4). , (0,4).
|
|
|