SOLUTION: Find the inverse of the matrix 1 1 4 4

Algebra ->  Matrices-and-determiminant -> SOLUTION: Find the inverse of the matrix 1 1 4 4      Log On


   

Question 935783: Find the inverse of the matrix
1 1
4 4
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Finding the Inverse of a 2x2 Matrix

To find the inverse of the matrix A=%28matrix%282%2C2%2C1%2C1%2C4%2C4%29%29, we can follow these steps:

Step 1) Find the determinant



The determinant of 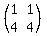%28matrix%282%2C2%2C1%2C1%2C4%2C4%29%29 is abs%28matrix%282%2C2%2C1%2C1%2C4%2C4%29%29=0. So this means that d=0

Since the determinant is equal to zero, this means that no inverse exists.

Remember, the inverse of 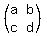%28matrix%282%2C2%2Ca%2Cb%2Cc%2Cd%29%29 is %281%2Fd%29%28matrix%282%2C2%2Cd%2C-b%2C-c%2Ca%29%29.

If d=0, then a division by zero occurs, which is NOT allowed.

So we can stop here.


=================================================================


Answer:

So the inverse of A=%28matrix%282%2C2%2C1%2C1%2C4%2C4%29%29 does NOT exist since d=0 (ie the determinant is 0).