|
Question 935598: One of two pipes can fill a pool 24 hours faster than the other one. The slower pipe filled the pool for 8 hours, then the other pipe was opened. The pipes filled together for 20 hours and filled 2/3 of the pool. Find the time that each pipe requires to fill the pool alone. Please help me to solve this complicated problem. I just know that the answer is 60 and 84 hours. But I am really eager to know how to solve it Thank you in advance )))
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One of two pipes can fill a pool 24 hours faster than the other one. The slower pipe filled the pool for 8 hours, then the other pipe was opened. The pipes filled together for 20 hours and filled 2/3 of the pool. Find the time that each pipe requires to fill the pool alone. Please help me to solve this complicated problem. I just know that the answer is 60 and 84 hours. But I am really eager to know how to solve it Thank you in advance )))
Let time faster pipe takes to fill pool, be T
Then time slower pipe takes is: T + 24
Thus, faster pipe can fill 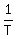 of pool in 1 hr, while slower pipe can fill of pool in 1 hr, while slower pipe can fill 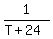 of pool in 1 hr of pool in 1 hr
Since slower pipe was turned on for 8 hours, by itself, and for 20 hours, with the faster pipe,
the slower pipe was turned on for a total of 28 (8 + 20) hours
Faster pipe was open for 20 hours
Therefore, we can say that:


28(3)(T) + 20(3)(T + 24) = 2(T)(T + 24) ------- Multiplying by LCD, 3(T)(T + 24)






(T – 60)(T + 12) = 0
T, or time faster pipe takes to fill pool is:  hours OR T = - 12 (ignore) hours OR T = - 12 (ignore)
Time slower pipe takes = 60 + 24, or  hours hours
You can do the check!!
===================
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|
| |