SOLUTION: find the point which divides the segment from (-5,-4) to (6,-2) in the ratio 2:3

Algebra ->  Angles -> SOLUTION: find the point which divides the segment from (-5,-4) to (6,-2) in the ratio 2:3      Log On


   

Question 935410: find the point which divides the segment from (-5,-4) to (6,-2) in the ratio 2:3
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
The ratio uses the distance between the given points in five equal parts, and you want 2%2F5 of this distance from one point to the other point.

Distance Formula! Unknown point between, (x,y).

Distance between given points, 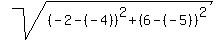sqrt%28%28-2-%28-4%29%29%5E2%2B%286-%28-5%29%29%5E2%29,
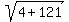
sqrt%284%2B121%29
sqrt%28125%29
highlight_green%285sqrt%285%29%29

Another way to take the rest of this is from (-5,-4) to (x,y) is 2 parts and from (x,y) to (6,-2) is 3 parts. Still two equations are needed.

---
sqrt%28%28x-%28-5%29%29%5E2%2B%28y-%28-4%29%29%5E2%29=%282%2F5%295%2Asqrt%285%29
sqrt%28%28x%2B5%29%5E2%2B%28y%2B4%29%5E2%29=2sqrt%285%29
highlight_green%28%28x%2B5%29%5E2%2B%28y%2B4%29%5E2=20%29
AND
sqrt%28%28x-6%29%5E2%2B%28x-%28-2%29%29%5E2%29=%283%2F5%295%2Asqrt%285%29
sqrt%28%28x-6%29%5E2%2B%28y%2B2%29%5E2%29=3%2Asqrt%285%29
highlight_green%28%28x-6%29%5E2%2B%28y%2B2%29%5E2=45%29
---

Instead of continuing to try to solve these two simultaneous quadratic equations in two variables, find and use the equation of the line containing the two given points!!
m=%28-2-%28-4%29%29%2F%286-%28-5%29%29=2%2F11
and pick second point,
y=%282%2F11%29x%2B%28-2-%282%2F11%29%2A6%29
y=%282%2F11%29x%2B%28-2-12%2F11%29
y=%282%2F11%29x%2B%28-22%2F11-12%2F11%29
highlight_green%28y=%282%2F11%29x-34%2F11%29

A large number of more arithmetic steps using some substitutions with this line equation. (unfinished here)