Find the coefficient of x^4 in the binomial expansion of (5+2x)^7
(with steps please)
Formula for a specific term in an expansion: (a + b)n = nCr-1(a)n-(r-1)(b)r-1, where r = term number
(5 + 2x)7
Observing the binomial, it’s seen that the x-term, or “b” in the expansion of the binomial needs to be to the 4th power.
Thus, the term that produces  is the term that needs to be determined. Thus, we can say that:
is the term that needs to be determined. Thus, we can say that:  , and that:
, and that:
4 = r – 1
4 + 1 = r
r, or term number = 5
Using the formula for a specific term in an expansion, term 5 or the 5th term can be determined, as follows:
(a + b)n = nCr-1(a)n-(r-1)(b)r-1, where r = term number
(5 + 2x)7 = 7C5-1(5)7-(5-1)(2x)5-1, where r = 5th term
(5 + 2x)7 = 7C4(5)7-4(2x)4
(5 + 2x)7 = 35(5)3(2x)4
(5 + 2x)7 = 4,375(16)x4
(5 + 2x)7 = 70,000x4
Thus, the  term, or 5th term of the binomial expansion:
term, or 5th term of the binomial expansion: 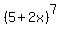 , is 70,000x4, which means
, is 70,000x4, which means
that the coefficient is 
Not to be confused, if the binomial's expressions were rearranged from 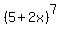 to
to 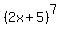 ,
,
then 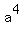 or
or 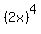 would be the 4th term.
would be the 4th term.
You can do the check!!
===================
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.