Question 935255: One part of a quartz crystal is a hexagonal prism with a right section of 1.5sq.cm. and edge of 2.3cm. If the base is a regular polygon and the largest circle that can be inscribed in it has a radius of 1.3cm, what is the altitude of the prism?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The bases are rather large, larger than the inscribed circle with a radius of 1.3cm, which has an area of
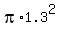     (rounded) . (rounded) .
The right section (a cross section perpendicular to the edges) is much smaller because it is not a right prism, meaning that the edges are not perpendicular to the bases. It is nor a right prism, but we do not call it a "wrong prism"; we call it an oblique prism.
We can calculate its volume as
(area of base)(height) , or as (area of right section)(edge length),
with compatible units, of course.
Both products are the same:
(area of base)(height) = (area of right section)(edge length) .
If we calculate the area of the base,
which is 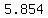   (rounded), (rounded),
we have 3 of the 4 factors.
Substituting we get
 ---> ---> ---> --->
 (rounded). (rounded).
The units are not shown, but we know what areas are in square cm and lengths (height and edge length) are in cm.
with that area, the area of right section, and the edge length,
we can calculate the height.
So, how did I calculate the area of the bases?
Each base, with its inscribed circle looks like this:

A regular hexagon with  sides can be split into sides can be split into  congruent equilateral triangles by connecting all the vertices with the center. congruent equilateral triangles by connecting all the vertices with the center.
The largest circle than can be drawn inside is tangent to each side of the hexagon at its midpoint,
so that the radius of such a circle is the height of those  triangles. That radius and its length are called the apothem of the hexagon. triangles. That radius and its length are called the apothem of the hexagon.
The apothem segment splits each of those  isosceles triangles into isosceles triangles into  30-60-90 right triangles. 30-60-90 right triangles.
We know that the red long leg of those triangles is  times as long as the short leg, times as long as the short leg,
so with a long leg measuring 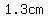 , the short leg measures , the short leg measures   , and the green hypotenuse (a side of the equilateral triangle is twice that long, measuring , and the green hypotenuse (a side of the equilateral triangle is twice that long, measuring 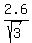  . .
The area of the equilateral triangle is
(long leg)(short leg) =
The area of that regular polygon can be calculated as the sum of the areas of all those triangles:
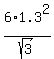   . .
|
|
|