You said "perfect NUMBER" last time you posted, not "perfect SQUARE"!
A perfect number is NOT a perfect square. Here it is with "perfect SQUARE".
However, you should have been able to tell from what I posted before that what
you do is add up the probabilities of whatever kinds of rolls you were told.
All I had to do below was to copy and paste my other solution, take out the
P(6), 6 was the perfect number, and add in P(4) and P(9), the perfect squares.
Here are all 36 possible rolls. Each sum occurs
on the diagonals that slant this way /:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
P(2)=1/36
P(3)=2/36
P(4)=3/36
P(5)=4/36
P(6)=5/36
P(7)=6/36
P(8)=5/36
P(9)=4/36
P(10)=3/36
P(11)=2/36
P(12)=1/36
[Everything is the same as before to here]
4 and 9 are the only perfect squares that can be thrown.
[This was the only difference]
2,3,5,7,11 are the primes that can be thrown.
P(perfect square or prime) = P(4)+P(9)+P(2)+P(3)+P(5)+P(7)+P(11) =
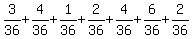I'm not going to add those up for you, you can do that yourself. I'm
here to explain how to do problems, not give you answers so you can
make a good grade on your homework and fail your tests. Teachers aren't
dumb. I was one for many years. I always knew when students got somebody
else to do their homework for them.
Edwin
