Question 935076: An arithmetic progression P consists of n terms. From the progression three different progressions P1, P2 and P3 are created such that P1 is obtained by the 1st, 4th, 7th .... terms of P, P2 has the 2nd,5th, 8th .....terms of Pand P3 has 3rd, 6th, 9th ..... terms of P. It is found that of P1, P2 and P3 two progressions have the property that their average is itself a term of the original progression P. Which of the following can be a possible value of n?
(a.) 20
(b.) 26
(c.) 36
(d.) Both 1 and 2
For the above question, if the Common difference between the terms of P1 is 6, what is the common difference of P?
(a.) 2
(b.) 3
(c.) 6
(d.) Cannot be determined
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the terms of  be be  , ,  , ... , with , ... , with  , ,  being the common difference between the terms od being the common difference between the terms od  . .
1) The average of  terms of an arithmetic progression is term number terms of an arithmetic progression is term number 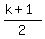 of that arithmetic progression if of that arithmetic progression if  is odd. is odd.
If 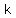 terms is the average of two consecutive terms in the middle of that progression (terms number terms is the average of two consecutive terms in the middle of that progression (terms number 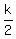 and and  ), and that is not a term of the arithmetic progression. ), and that is not a term of the arithmetic progression.
If  has an odd number of terms, the average of all the terms of has an odd number of terms, the average of all the terms of  will be a term of will be a term of  and a term of and a term of  . .
If  has an even number of term its average will be the average of two consecutive terms of has an even number of term its average will be the average of two consecutive terms of  that would be terms that would be terms 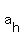 and and 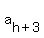 of of  . .
In  , after , after 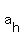 comes comes  , ,  , and {{a[h+3]=a[h]+3d}}} . The average of , and {{a[h+3]=a[h]+3d}}} . The average of 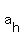 and and 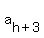 would be would be
 . .
That is a number between 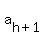 and and 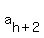 , and is not a term of , and is not a term of  . .
In sum, if  has an odd number of terms, the average of its terms is a term of has an odd number of terms, the average of its terms is a term of  and a term of and a term of  ; if ; if  has an even number of terms, the average of its terms is neither a term of has an even number of terms, the average of its terms is neither a term of  nor a term of nor a term of  . .
The same can be said of  and and 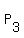 . .
If  has has  terms, terms, 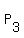 will have will have  terms, terms,
starting with term number  of of  , and ending with term number , and ending with term number  of of  . .  and and  will also have will also have  terms, because terms, because  starts and ends starts and ends  terms of terms of  before before 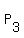 , and , and  starts and ends starts and ends  terms of terms of  before before 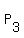 . In that case, all four arithmetic progressions will have an even number of terms, and will have averages that are not terms of . In that case, all four arithmetic progressions will have an even number of terms, and will have averages that are not terms of  . .
If  were were  less, less, 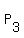 would have would have  less, but less, but  and and  would still have would still have  terms. That happens for all terms. That happens for all  that are that are  short of a multiple of short of a multiple of  , such as , such as
 and and  . .
For  , , 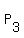 has 6 terms, but has 6 terms, but  and and  have have  terms. The averages for terms. The averages for  and and  are their respective 4th terms, that are terms of are their respective 4th terms, that are terms of  . .
The same thing happens for  , which gives , which gives  and and   terms and their averages are their respective 5th terms. terms and their averages are their respective 5th terms.
So, the answer is (d.) Both 1 and 2.
2) The common difference for terms of  , ,  and and  is the same. It is the difference between terms is the same. It is the difference between terms 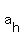 and and 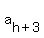 of of  . .
If that is  , ,
 ---> ---> ---> --->
|
|
|