SOLUTION: Solve using Cramer’s rule 3x-y+2z=13, 2x+y-z=3, x+3y-5z=-8

3x-y+2z=13 
2x+y-z=3 
x+3y-5z=-8

Below is one solved exactly like yours. Use it as a model to solve 
yours.

Whenever one of your equations has x with coefficient 1 or -1,
it makes it easier to write that equation first. Since your 
3rd equation has x with an understood coefficient of 1, it will 
be easier if you write it first, like this, swapping the 1st and 
3rd equations so that it is at the top.

x+3y-5z=-8
2x+y-z=3
3x-y+2z=13

BTW, yours has solution (x,y,z) = (3,-2,1)
  
----------------------------------
Here's one just like yours. Just use your numbers instead:

x+y+z=6
2x-y+z=3
x+2y-3z=-4

To solve using Cramer's rule
 
Write in all the 1 and -1 coefficients:



There are 4 columns,
 
1. The column of x-coefficients 
 
2. The column of y-coefficients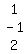 
 
3. The column of z-coefficients  
 
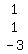4. The column of constants:     
 
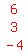There are four determinants:
 
1. The determinant  consists of just the three columns
of x, y, and z coefficients. in that order, but does not
contain the column of constants.
 
. 
 
It has value .  I'm assuming you know how to find the
value of a 3x3 determinant, for that's a subject all by itself.
If you don't know how, post again asking how. 
 
2. The determinant  is like the determinant 
except that the column of x-coefficients is replaced by the
column of constants.   does not contain the column 
of x-coefficients.
 
.
 
It has value .
 
3. The determinant  is like the determinant 
except that the column of y-coefficients is replaced by the
column of constants.   does not contain the column 
of y-coefficients.
 
.
 
It has value .
 
4. The determinant  is like the determinant 
except that the column of z-coefficients is replaced by the
column of constants.   does not contain the column 
of z-coefficients.
 
.
 
It has value .
 
Now the formulas for x, y and z are
 




[To read about the 18th century Swiss mathematician Gabriel Cramer 
who invented Cramer's rule, go here: 
http://en.wikipedia.org/wiki/Gabriel_Cramer
 
Edwin