SOLUTION: {{{cot^-1(1/sqrt(3))}}}

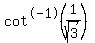
That says:

Draw an equilateral triangle with all three sides equal to 2.
Its angles are all 60°:

Cut it in half by drawing an altitude of length h, into two 
congruent right triangles. It cuts the bottom side in half, each 
half measures 1 each.



Eliminate the right half:



Calculate h by the Pythagorean theorem:



Write  instead of h:



Now return to the original problem:

We know that .  Since the

numerator of  is 1 and the denominator is ,

we see that 60° is the angle whose cotangent is .

In radians that's .

Edwin