SOLUTION: Simplify without using tables or calculators.sin^2 495degrees(1-tan^2 780degrees/(1 cos^2 600degrees)(1 tan^ 570degrees)

Algebra ->  Trigonometry-basics -> SOLUTION: Simplify without using tables or calculators.sin^2 495degrees(1-tan^2 780degrees/(1 cos^2 600degrees)(1 tan^ 570degrees)      Log On


   

Question 934973: Simplify without using tables or calculators.sin^2 495degrees(1-tan^2 780degrees/(1 cos^2 600degrees)(1 tan^ 570degrees)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I suspect that what you mean may have been
sin^2 (495degrees)(1-tan^2 (780degrees))/(1 - cos^2 (600degrees))(1-tan^2) 570degrees))= ,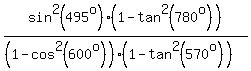
but whatever the operations among those trigonometric functions,
the expression's value is much simpler than it looks.
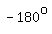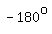The key is to find a more familiar/convenient co-terminal angle (one that differs by one or more turns in either direction). I aim for one between -180%5Eo and -180%5Eo .
From there, you look for a reference angle in the first quadrant.
The reference angle is one with a symmetrical terminal side. All trigonometric have the same absolute value for the reference angle, so you just have to worry about the sign. (And if all ther trigonometric functions in your expression are squared, you do not even have to worry about the sign.

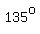495%5Eo=360%5Eo%2B135%5Eo so sin%28495%5Eo%29=sin%28135%5Eo%29 ,
and 135%5Eo is an angle in the second quadrant
that is symmetrical to 180%5Eo-135%5Eo=45%5Eo ,
so sin%28495%5Eo%29=sin%28135%5Eo%29=sin%2845%5Eo%29=sqrt%282%29%2F2=sqrt%281%2F2%29 ,
and sin%5E2+%28495%5Eo%29=%28sqrt%281%2F2%29%29%5E2=1%2F2

780%5Eo=720%5Eo%2B60%5Eo=2%28360%5Eo%29%2B60%5Eo so tan%28780%5Eo%29=tan%2860%5Eo%29=sqrt%283%29 ,
so tan%5E2+%28780%5Eo%29=%28sqrt%283%29%29%5E2=3 ,
and %281-tan%5E2+%28780%5Eo%29%29=1-3=-2 .

600%5Eo=720%5Eo-120%5Eo so cos%28600%5Eo%29=cos%28-120%5Eo%29 ,
and -120%5Eo is an angle in the third quadrant,
that is symmetrical to 120%5Eo in the second quadrant,
and to 180%5Eo-120%5Eo=60%5Eo in the first quadrant.
cos%28600%5Eo%29=cos%28-120%5Eo%29=cos%28120%5Eo%29=-cos%2860%5Eo%29=-1%2F2 .
Then, cos%5E2%28600%5Eo%29=%28-1%2F2%29%5E2=1%2F4 and 1-cos%5E2%28600%5Eo%29=1-1%2F4=3%2F4 .

570%5Eo=360%5Eo%2B210%5Eo and 210%5Eo=180%5Eo%2B30%5Eo ,
so the reference angle for 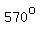570%5Eo+ is 30%5Eo ,
and tan%28570%5Eo%29=tan%2830%5Eo%29=sqrt%283%29%2F3=sqrt%281%2F3%29 .
Then, tan%5E2%28570%5Eo%29=%28sqrt%281%2F3%29%29%5E2=1%2F3 and
1-tan%5E2%28570%5Eo%29=1-1%2F3=2%2F3 .

So if your expression was 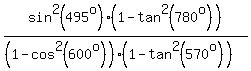,