Question 934943: One leg of a right triangle has length 7. The lengths of the other two sides are whole numbers. The length of the other leg is ? and the length of the hypotenuse is ?
Found 2 solutions by KMST, MathLover1:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The length of the other leg is  and the length of the hypotenuse is and the length of the hypotenuse is  . .
Sets of 3 integers that could be lengths of the sides of a right triangle are called Pythagorean triples.
The only one I remember is {3, 4, 5} , but I looked up a list online and {7, 24, 25} was the only set with a 7 in it.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! let sides be  , ,  and and 
If it is a right angle triangle, then the relationship between the sides must follow the Pythagorean theorem:

Obviously, the side called  must be the longest one (because squares can never be negative). must be the longest one (because squares can never be negative).
Let's get rid of the "degenerate" solution of



(this is called a "degenerate" triangle because one side measures  ) )
(mathematically, it could still be a triangle, but in real life, it is simply a line segment)
You are looking for a solution where one side is  and the other two sides are and the other two sides are   . .
We know that there are no solutions if you use 
Next, you can check values where 
(you don't need to check  because it will be the same exercise) because it will be the same exercise)


The "formula" to find the difference between two squared integers goes like this

for example

let's check



(this is not a coincidence, there is a true reason why this "trick" works).
So we need two numbers such that the difference of their squares is 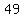

because we need the two end numbers, the smallest difference would be  and and 
because 

let's try



There is a triangle  , ,  , ,  would be a right-angle triangle with three sides being would be a right-angle triangle with three sides being   and one side being and one side being  . .
|
|
|