SOLUTION: what is the sum of 2+3+5+6+8+9+....2n terms?

Algebra ->  Sequences-and-series -> SOLUTION: what is the sum of 2+3+5+6+8+9+....2n terms?      Log On


   

Question 934667: what is the sum of 2+3+5+6+8+9+....2n terms?
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
I think the "2n terms" should have been "3n terms", because with 
2n terms, there will have to be three formulas, depending on whether 
2n is a multiple of 3, 1 less than a multiple of 3, or 1 more than 
a multiple of 3.

So I'm going to do the problem assuming that the 2n should have been 3n,

OK?  Let me know.

It's the sum of two arithmetic sequences:

S1 = 2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+...+3n+1 (to 3n terms) 
S2 =    -4    -7    -10      -13      -16+...      (to n terms   

There are 3n terms of the first sequence and n terms of the second sequence.

We use the formula:

S%5Bn%5D=expr%28n%2F2%29%28a%5B1%5D%2Ba%5Bn%5D%29

We substitute 3n for n, a%5B1%5D=2, a%5B3n%5D=3n%2B1

S1%5B3n%5D=expr%283n%2F2%29%282%2B3n%2B1%29
S1%5B3n%5D=expr%283n%2F2%29%283n%2B3%29
S1%5B3n%5D=expr%283n%2F2%29%283%28n%2B1%29%29
S1%5B3n%5D=expr%289n%2F2%29%28n%2B1%29 
S1%5B3n%5D=9n%28n%2B1%29%2F2 = the sum of the 1st sequence.

We use the formula 

S%5Bn%5D=expr%28n%2F2%29%282a%5B1%5D%2B%28n-1%29d%29

to find the sum of the 2nd sequence

a%5B1%5D=-4, d=-3 

S2%5Bn%5D=expr%28n%2F2%29%282%28-4%29%2B%28n-1%29%28-3%29%29
S2%5Bn%5D=expr%28n%2F2%29%28-8-3n%2B3%29%29
S2%5Bn%5D=expr%28n%2F2%29%28-5-3n%29%29
S2%5Bn%5D=n%28-5-3n%29%29%2F2
S2%5Bn%5D=-n%285%2B3n%29%29%2F2

So the required sum is

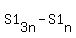
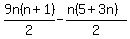
S1%5B3n%5D-S1%5Bn%5D%22%22=%22%229n%28n%2B1%29%2F2-%28n%285%2B3n%29%29%2F2%22%22=%22%22

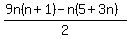
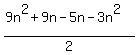
%289n%28n%2B1%29-n%285%2B3n%29%29%2F2%22%22=%22%22%289n%5E2%2B9n-5n-3n%5E2%29%2F2%22%22=%22%22

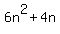
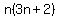6n%5E2%2B4n%29%2F2%22%22=%22%223n%5E2%2B2n%22%22=%22%22n%283n%2B2%29

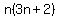Sum of the first 3n terms = n%283n%2B2%29

Edwin