SOLUTION: sin(2x)+cos(x)=1

Algebra ->  Trigonometry-basics -> SOLUTION: sin(2x)+cos(x)=1       Log On


   

Question 934303: sin(2x)+cos(x)=1

Answer by AnlytcPhil(1807) About Me  (Show Source):
You can put this solution on YOUR website!
sin%282x%29%2Bcos%28x%29=1

2sin%28x%29cos%28x%29%2Bcos%28x%29=1

Substitute 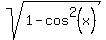sqrt%281-cos%5E2%28x%29%29 for sin%28x%29

2sqrt%281-cos%5E2%28x%29%29cos%28x%29%2Bcos%28x%29=1

2sqrt%281-cos%5E2%28x%29%29cos%28x%29=1-cos%28x%29

Square both sides:

4%281-cos%5E2%28x%29%29cos%5E2%28x%29=1-2cos%28x%29%2Bcos%5E2%28x%29

4cos%5E2%28x%29-4cos%5E4%28x%29=1-2cos%28x%29%2Bcos%5E2%28x%29

-4cos%5E4%28x%29%2B3cos%5E2%28x%29%2B2cos%28x%29-1+=+0

4cos%5E4%28x%29-3cos%5E2%28x%29-2cos%28x%29%2B1+=+0

1 | 4  0  -3  -2  1
  |    4   4   1 -1  
    4  4   1  -1  0

So we have factored the polynomial in cos(x) as



cos%28x%29-1=0,  4cos%5E3%28x%29%2B4cos%5E2%28x%29%2Bcos%28x%29-1+=+0
cos%28x%29=1
x=2pi%2An, n any integer.  That's one solution

4cos%5E3%28x%29%2B4cos%5E2%28x%29%2Bcos%28x%29-1+=+0

That has no rational roots.  Solving it using a TI-84
calculator, we get

cos%28x%29=0.3478103848
x=1.215561666%2B2pi%2An

But since we had to use a calculator to get the second
answer, we may as well have solved the whole thing by
using the graphing calculator in the first place.

Edwin