Question 93383: please perform the indicated operation (5x-6)(5x-6) the university of phoenix elementary and intermediate algebra
Found 2 solutions by bucky, Edwin McCravy:
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given:
.
(5x - 6)(5x - 6)
.
The given operation is multiplication and you have two quantities to multiply. Each quantity
is in its own set of parentheses.
.
This problem is of the form (a + b)(c + d) and you can do it by taking the first term in the
set of parentheses and using it to multiply each of the two terms in the second set of
parentheses. Then take the second term in the first set and use it to multiply each term
in the second set of parentheses. Finally you collect all the products and combine them as
rules permit. So using this process, you would first take "a" and use it to multiply
(c + d). The result would be a*c + a*d. Then you would take the second term, "b", and use it
to multiply (c + d). The result would be b*c + b*d. So you would have four answers to
combine ... ac + ad + bc + bd.
.
Once you get familiar with this process the pattern will come to you naturally, and the
pattern will make sense.
.
Now let's return to the problem you were given and apply this pattern to it:
.
(5x - 6)(5x - 6)
.
From the first (left hand) set of parentheses take the 5x and use it to multiply both terms
in the second set of parentheses. The products are (5x)*(5x) and (5x)(-6) and the two
results are 25x^2 and -30x.
.
Next, from the first (left hand) set of parentheses take the -6 and use it to multiply both
terms in the second set of parentheses. The products are (-6)*(5x) and (-6)*(-6) and the
two results are -30x and + 36.
.
So all four products are 25x^2 - 30x - 30x + 36. Notice that the two -30x terms can be added
together to get -60x. Therefore, the final answer is:
.
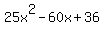
.
Hope this helps you to understand the process and a pattern you can use to multiply
two binomials.
.
You can use the same general procedure to multiply a binomial times a trinomial, two trinomials,
and so forth.
.
For example ... to multiply (a + b)*(c + d + e) which is multiplying a binomial times a trinomial
you just take (one at a time) the two terms in the binomial and multiply them times each
term in the trinomial. So the products you would get are a*c, then a*d, then a*e. Once
you are that far, you take the second term of the binomial and multiply it times each of the
three terms in the trinomial to get b*c, then b*d, then b*e. You then have 6 products as
follows: a*c + a*d + a*e + b*c + b*d + b*e
.
All you have to do then is to see if any of the products can be combined with other products.
Do all the possible combinations and the resulting terms are the answer.
.
In shortened form ... multiply (a + b + c) times (d + e + f) ...
.
The products are a*d + a*e + a*f + b*d + b*e + b*f + c*d + c*e +c*f
.
Then all you do is look at these 9 answers and combine all the like terms you can find to
get the final answer. This may give you a better feel for how the pattern works and the
process of taking the terms in the first set of parentheses one at a time and using them to
multiply each of the terms in the second set of parentheses to come up with the answer.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(5x-6)(5x-6)
This is called "FOIL" for Firsts, Outers, Inners, Lasts
(5x-6)(5x-6)
Multiply the FIRSTS, that is, the first red 5x in the
parentheses on the left by the blue 5x in the
parentheses on the right, which gives 25x². Write
this down:
25x²
(5x-6)(5x-6)
Multiply the OUTERS, that is, the terms on the outer
ends, that is, the red 5x on the far left by the green -6
on the far right, which gives -30x. Write this down
next to the 25x²:
25x²-30x
(5x-6)(5x-6)
Multiply the INNERS, that is, the terms on the inside,
that is, the purple -6 by the blue 5x, which also gives
-30x. Write this down next to the other -30x:
25x²-30x-30x
(5x-6)(5x-6)
Multiply the LASTS, that is, the last purple -6 in the
parentheses on the left by the last green -6 in the
parentheses on the right, which gives +36. Write
this down next to the -30x:
25x²-30x-30x+36
Now the middle two terms are like terms, so we
can combine them as -60x:
25x² - 60x + 36.
Edwn
|
|
|