Question 933569: we have to arrange chairs for the audience a in the first row we can place 20 chairs in the next 22 chairs 2 chairs can be added to each row than the previous one we have to arrange 50 so how many chairs are needed WE HAVE TO USE AP FORMULA
(arithmetic progression)
so how many chairs will be in the 25th row?
with thousand how many perfect rows can you make?
how many chairs will be in the last row?
what are the difference in the number of chairs for arranging 25 rows and 50 rows?
in which row 50 chairs will exist?
will you be able to make perfect rows with thousand chairs? if not how many chairs are needed to make the row perfect?
if you need to make 2 more rows how more chairs are needed?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! # of chairs in rows: 20, 22,24,26,28,30,32,34,36,38,40,42,44,46,48,50
difference 


a.
how many chairs will be in the 25th row?


 ...chairs will be in the 25th row ...chairs will be in the 25th row
b.
with  chairs how many perfect rows can you make chairs how many perfect rows can you make





 .....# of rows you can make, since .....# of rows you can make, since 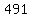 is NOT a perfect number, is NOT a perfect number,
the only perfect numbers between  and and  are are  , , 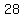 , , 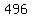 ; since ; since 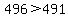 , with , with  chairs you can make only chairs you can make only  perfect rows which are rows perfect rows which are rows  and and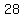
c.
how many chairs will be in the last row?
the last row is  : :
 ...# chairs in the last row ...# chairs in the last row
d.
what are the difference in the number of chairs for arranging 25 rows and 50 rows?
 ...chairs will be in the 25th row ...chairs will be in the 25th row




the difference in the number of chairs for arranging  rows and rows and  rows is rows is 
or, since the difference in the number of chairs for arranging between two rows is 2 chairs, then
between  rows and rows and  will be will be 
e.
in which row  chairs will exist? chairs will exist?




 .....row in which .....row in which  chairs will exist chairs will exist
f.
will you be able to make perfect rows with thousand chairs? if not how many chairs are needed to make the row perfect?
from c. we know that
 and and 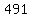 is not perfect row because is not perfect row because 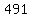 is NOT a perfect number is NOT a perfect number
first perfect number is  (see b.); so we need 5more rows or 10 more chairs (see b.); so we need 5more rows or 10 more chairs




g.
if you need to add  more rows you will have more rows you will have 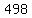 rows rows
as given,for each additional row you need  more chair; so, to make more chair; so, to make  more rows you will need more rows you will need  more chairs to row more chairs to row 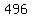 which is which is 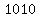 ; so, we will have ; so, we will have  chairs in row # chairs in row # 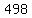
check:






 ...so, we got a row number ...so, we got a row number 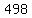
|
|
|