Question 933044: How would I roughly sketch and show Y and X Intercepts: P(X)= 2x^3-x^2+x
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Choose the case level and stay with it.
 . .
Three roots.
The quadratic factor's roots:
 and and 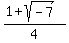 , not Real. , not Real.
The only real root is x=0.
The basic shape is that p decreases toward the left without bound and increases toward the right without bound. Between the extreme regions needs more attention.
Near x=0:
Look at -1 and +1 to help near this.
At x=-1, p is 2(-)-(+)+(-), or p is (-)+(-)+(-), meaning 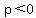 when when  . .
Look at x=1, p is 2(+)-(+)+(+), not too clear.
Try at x=(1/2). p=2(1/8)-1/4+1/2=1/4-1/4+1/2=1/2, which is positive.
The function CROSSES the x-axis at x=0.
Derivative calculus would be helpful for further details.
 . .
The roots of this will be the extreme points for p(x).
Can you handle this part of the work?
Jumping ahead, this is the graph:

Also, find the discriminant of the derivative. Is it negative? That tells you something.... Notice, the graph has no minimum or maximum.
|
|
|