Question 932669: Please explain the method used to solve these:
Solve triangle ABC. (If an answer does not exist, enter DNE. Round your answers to one decimal place.)
b = 67, c = 38, ∠A = 78°
∠B =____°
∠C =____°
a = ____
---------------------------------------
Solve triangle ABC. (If an answer does not exist, enter DNE. Round your answers to one decimal place.)
a = 17, b = 19, c = 25
∠A =____°
∠B =____°
∠C =____°
THANKS!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Right triangles are easy,
and can be solved with just the Pythagorean theorem,
and the definition of sine and cosine as trigonometric ratios.
You probably remember those
However, not all triangles are right triangles,
and to solve any triangles there are 2 tools:
the law of sines, and the law of cosines.
IN CASE YOU HAVE TROUBLE REMEMBERING "LAWS":
The law of sines goes a little further than the fact that a longer side is opposite a larger angle, and gets into the issue of how much longer, and how much larger.
The law of sines says that in a triangle the ratio of the sine of an angle to the length of the opposite side is constant.
In formula, if sides a, b, and c are opposite angles A, B, and C respectively,
 or or  . .
To be able to use the law of sines, you need to have the measure of an angle and the length of the opposite side.
As a consequence, the law of sines does not solve your problems.
You will have to use the law of cosines.
The law of cosines is kind of an extension of the Pythagorean theorem.
The Pythagorean theorem theorem says that
if  and and  are the lengths of the legs of a right triangle, are the lengths of the legs of a right triangle,
and  is the length of the hypotenuse, is the length of the hypotenuse,
 . .
In a triangle with sides of lengths  and and  , ,
forming an angle  , the length , the length  of the opposite angle of the opposite angle 
may be such that  is more or less than is more or less than  . .
If C is an acute angle, with 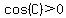 , ,  is less than is less than  . .
How much less?
The difference is not only proportional to 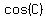 , but also to side lengths , but also to side lengths  and and  , and that makes sense. , and that makes sense.
In fact,  , and that is the law of cosines. , and that is the law of cosines.
If  is an obtuse angle is an obtuse angle  , ,
and the term 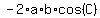 is positive, making is positive, making 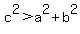 . .
Of course, for the law of cosines, side  and opposite angle and opposite angle  can be any of the 3 side/angle pairs, no matter what letter they are called. can be any of the 3 side/angle pairs, no matter what letter they are called.
THE PROBLEMS:
 , ,  , , 
Since the name of the angle given is  , ,
we write the law of cosines as
 . .

Using the approximate value 
(or using however many digits your calculator will use)
we can find  and then and then  . .


 (rounded) (rounded)
 ---> ---> (rounded) (rounded)
Now that you have  , ,  , ,  and and  , ,
you can use law of sines to find  and and  , ,
and that is what I would do.
(you could also keep using law of cosines)
Substituting into  we get we get

 ---> ---> ---> ---> (rounded)---> (rounded)---> (rounded) (rounded)
 ---> ---> ---> ---> (rounded)---> (rounded)---> (rounded) (rounded)
 , ,  , , 
 <---> <---> <---> <---> can be used to find can be used to find 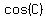 } and from there } and from there  . .


 ---> ---> (rounded)---> (rounded)---> (rounded) (rounded)
From there you could try law of sines to find  and and  , ,
but in this case, using law of cosines for everything seems easier to me.
We can switch the letters around and use law of cosines to calculate
 and and  . .



 ---> ---> } (rounded)---> } (rounded)---> (rounded) (rounded)



 ---> ---> (rounded)---> (rounded)---> (rounded) (rounded)
|
|
|