Question 932490: What is the measure of the angle formed by the bisectors of two angles of an equilateral triangle?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! recall properties:
-The interior angles of a triangle always add up to  .° .°
-Because the interior angles always add to  °, every angle must be less than °, every angle must be less than  ° °
-The 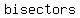 of the three interior angles meet at a point, called the of the three interior angles meet at a point, called the 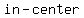 , which is the center of the , which is the center of the 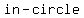 of the triangle. of the triangle.
by definition an equilateral triangle is a triangle which has all three of its sides  in in  , and all three angles of an equilateral triangle are always , and all three angles of an equilateral triangle are always  ° °
in an equilateral triangle, the median, angle bisector, and altitude are equal also, they intersect at point 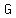 , the center of the inscribed and circumscribed circle , the center of the inscribed and circumscribed circle
each of the angles are divided by the bisector (a line which cuts an angle into two equal halves ) in two angles of  ° °
if the intersection of two bisectors is point 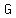 , and a triangle , and a triangle  , ,
a triangle formed by two bisectors and one side of triangle is 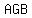 and angle and angle 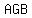
so,the measure of the angle 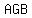 is: is:
 < <  ° °
|
|
|