Question 932086: How would I go about solving 49x^2 + y^2 = 49 finding the center, vertices, co- vertices and foci?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  ........both sides divide by ........both sides divide by 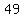

 => you have an ellipse; compare it to the standard form equation of an ellipse which is => you have an ellipse; compare it to the standard form equation of an ellipse which is  (your example is an ellipse with Vertical Major Axis,because (your example is an ellipse with Vertical Major Axis,because 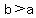 ) where ( ) where ( , , ) is the center, ) is the center,  is semiminor axis length, is semiminor axis length,  is semimajor axis length is semimajor axis length
Ellipses are actually very special cases of circles.
REMEMBER:
The right side of the equation must be  in order to be in standard form. in order to be in standard form.
The point ( , , ) is most commonly referred to as the CENTER. ) is most commonly referred to as the CENTER.
In order to graph an ellipse, you need  points: points:
Right point (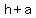 , , ) )
Left point (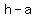 , , ) )
Top point ( , ,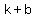 ) )
Bottom point ( , ,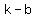 ). ).
in your case:
center at ( , , ) )
foci | (( , ,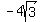 ) | ( ) | ( , , 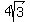 ))approx.(( ))approx.(( , ,  ) | ( ) | ( , ,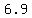 )) ))
vertices | ( , , ) | ( ) | (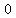 ) )
semimajor axis length | 
semiminor axis length |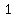
eccentricity | (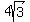 ) approx. ) approx.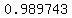

|
|
|