SOLUTION: Please help me solve this problem: Hiking Staff magazine says that the average hiker experiences a grade of 0.03 or less as flat. The Main Range Trail ascends eastbound out of

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: Please help me solve this problem: Hiking Staff magazine says that the average hiker experiences a grade of 0.03 or less as flat. The Main Range Trail ascends eastbound out of      Log On


   

Question 931525: Please help me solve this problem:
Hiking Staff magazine says that the average hiker experiences a grade of 0.03 or less as flat. The Main Range Trail ascends eastbound out of Yakker's Lake according to H(x)= 0.75+(2/5)Log(x+1), where x is elapsed distance in miles eastbound from the lake, and H(x) is miles above the elevation of the lake.
Mathematics Enthusiast magazine reports that the slope of form
y=C+kLogb(x+1) is k/lnb*(1/x+1)for any positive value of x. In this context, "Grade and "Slope" are synonyms.
Fred an average hiker, hikes eastbound out of Yakker's Lake. How far east of Yakker's Lake does Fred begin to think he is hiking on the flat?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The way I understand the problem, the Main Range Trail ascends eastbound out of Yakker's Lake according to
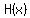H%28x%29=+0.75%2B%282%2F5%29log%28%28x%2B1%29%29 ,
where x is elapsed distance in miles eastbound from the lake,
H%28x%29 is miles above the elevation of the lake,
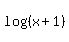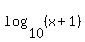and log%28%28x%2B1%29%29 is log%2810%2C%28x%2B1%29%29 , the common logarithm (base 10 logarithm) .
I also understand that Mathematics Enthusiast magazine reports that the slope of the graph for a function of the form
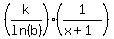y=C%2Bk%2Alog%28b%2C%28x%2B1%29%29 is %28k%2Fln%28b%29%29%2A%281%2F%28x%2B1%29%29 for any positive value of x.

H%28x%29=+0.75%2B%282%2F5%29log%2810%2C%28x%2B1%29%29 is a function of the form y=C%2Bk%2Alog%28b%2C%28x%2B1%29%29 ,
with C=0.75 , b=10 , and k=2%2F5=0.4 ,
so the slope of its graph is given by
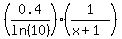%280.4%2Fln%2810%29%29%2A%281%2F%28x%2B1%29%29 .
So, the slope/grade of the trail east of Yakker's Lake is represented by the function
grade=0.4%2F%28ln%2810%29%2A%28x%2B1%29%29 .

Fred begin to think he is hiking on the flat when grade=0.03 , so our equation is
0.03=0.4%2F%28ln%2810%29%2A%28x%2B1%29%29 .
Solving:
0.03=0.4%2F%28ln%2810%29%2A%28x%2B1%29%29
0.03%2A%28x%2B1%29=0.4%2Fln%2810%29
x%2B1=0.4%2F%28ln%2810%29%2A0.03%29
x=0.4%2F%28ln%2810%29%2A0.03%29-1
Using the approximate value ln%2810%29=2.3026
(or using however many digits my calculator can handle),
x=4.79 (rounded).
So, Fred starts thinking the trail is flat when he is 4.8 miles east of the lake.