|
Question 930689: Find the smallest natural number that is simultaneously the sum of 9, 10 and 11
consecutive integers.
Found 2 solutions by mananth, greenestamps:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let first term be a1
d=1
Sn = n/2(a+l) .... l is the last term a is the first term
S9 = 9/2(1+9) =45
S10 = 10/2(1+10) =55
S11= 11/2 (1+11) = 66
Add them up 45+55+66 thats your answer
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor has nothing to do with the given problem....
Let the three strings of consecutive integers be
a(1), ..., a(9)
b(1), ..., b(10)
c(1), ..., c(11)
The sum of the each sequence is the number of terms in the sequence, multiplied by the average of the first and last terms.
First sequence...
The average of 9 consecutive integers is an integer;
The sum is 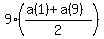
Second sequence...
The average of 10 consecutive integers is not an integer, but the sum of the first and last integers is an integer;
The sum is  = = 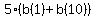
Third sequence...
The average of 11 consecutive integers is an integer;
The sum is 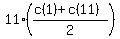
The three sums are to be the same; that means the sum must be a multiple of 9, 5, and 11. The least common multiple of 9, 5, and 11 is 495; and that is the answer to the problem.
First sequence: 495 = 9(55) = 51+52+...+58+59
Second sequence: 495 = 10(49.5) = 5(99) = 45+46+...+53+54
Third sequence: 495 = 11(45) = 40+41+...+49+50
ANSWER: 495
|
|
|
| |