Question 930337: Consider a list of randomly generated 4-letter "words" printed on a paper. The letters cannot be repeated.
(a) At least how many of these "words" should be printed to be sure of having at least 7 identical "words" on the list?
(b) At least how many identical "words" are printed if there are 2870401 "words" on the list?
Found 2 solutions by KMST, Edwin McCravy:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a) With the 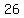 letters we use in the USA, we can form letters we use in the USA, we can form
 different "words" with no repeated letters. different "words" with no repeated letters.
If a list has  such "words", such "words",
it could contain exactly  repeats of each of those "words", repeats of each of those "words",
but not have any of them repeated  times. times.
However, a list with  such "words" such "words"
must have at least of of them repeated  or more times. or more times.
(b) If there are 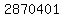 "words" on a list of 4-letter sequences made of 4 different letters, "words" on a list of 4-letter sequences made of 4 different letters,
all the 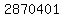 "words" could be ABCD, so I would say there is at least (((1))) repeated word. "words" could be ABCD, so I would say there is at least (((1))) repeated word.
However, if what the question means to ask is what is the maximum number of repetitions in that list,
 , ,
meaning that when you divide,
you get a quotient of  and a remainder of and a remainder of  , ,
or in other words  . .
That means that to have words repeated as few times as possible,
we need to repeat each of the 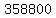 words words  times, times,
and then include an extra repetition of one of those words,
that would be repeated  times. times.
Any list length between  and and 
would have at least  repetitions of one or more words. repetitions of one or more words.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a) At least how many of these "words" should be printed to be sure of having at
least 7 identical "words" on the list?
There are 26 ways to choose the first letter, 25 to choose the 2nd letter, 24
ways for the 3rd and 23 for the 4th, so there are 26*25*24*23 = P(26,4)= 358800
possible "words".
If there were 6*358800 or 2152800 words on the list, there would be a very
slight chance that there were exactly 6 duplicates of each word. However to
eliminate that rare case, if there were 1 more word, or 2152801, on the list,
there would necessarily be 7 duplicates of some word.
Answer: 2152801.
(b) At least how many identical "words" are printed if there are 2870401 "words"
on the list?
We divide 2870401 by 358800
8
358800)2870401
2870400
1
We get 8 with 1 remainder.
So there is a slight chance that the 2870401 consists of exactly 8 duplicates of
each of the 358800 words, plus 1 more word. So there are at least 9 duplicates
of some word on the list.
Edwin
|
|
|