prove that the sum of all natural numbers divisible by 5 is equal to 5n(n+1)/2 using mathematical induction.
First we want to show that
if n were some integer for which the formula  gives the sum of
the first n positive multiples of 5, from 5 through 5n, then the same formula
with (n+1) substituted for n, would give the sum of the first n+1 positive
multiples of 5, from 5 up to 5(n+1).
Let's hypothetically suppose that n is some integer for which the formula
gives the sum of
the first n positive multiples of 5, from 5 through 5n, then the same formula
with (n+1) substituted for n, would give the sum of the first n+1 positive
multiples of 5, from 5 up to 5(n+1).
Let's hypothetically suppose that n is some integer for which the formula
 gives the sum of the first n positive multiples of 5
If that were the case then if we added 5(n+1) to it we would have the sum
of the first n+1 multiples of 5. So let's add 5(n+1) to the formula to see if
we get the formula
gives the sum of the first n positive multiples of 5
If that were the case then if we added 5(n+1) to it we would have the sum
of the first n+1 multiples of 5. So let's add 5(n+1) to the formula to see if
we get the formula  with n+1 substituted for n.
When we add them we get:
with n+1 substituted for n.
When we add them we get:


 We get an LCD:
We get an LCD:


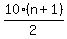
 We factor out (n+1) on top:
We factor out (n+1) on top:
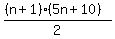 We factor out 5 from the second paretheses on top:
We factor out 5 from the second paretheses on top:
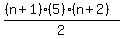
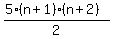 And now we see if this is what we'd get if we substituted n+1 for
n in the formula
And now we see if this is what we'd get if we substituted n+1 for
n in the formula  , so we substitute n+1 for n in it
to see:
, so we substitute n+1 for n in it
to see:

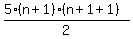
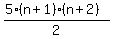 Yes that is what we got.
So therefore if we can find a value of n for which the formula
Yes that is what we got.
So therefore if we can find a value of n for which the formula
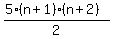 will give the sum of the first n positive
multiples of 5, then it will also give us the sum of the first
n+1 positive multiples of 5.
So all that's left is to find such a value of n.
Let's try n=1 to see if the formlaq holds for that:
will give the sum of the first n positive
multiples of 5, then it will also give us the sum of the first
n+1 positive multiples of 5.
So all that's left is to find such a value of n.
Let's try n=1 to see if the formlaq holds for that:

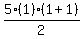
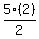

 Indeed it works for n=5 because the first positive multiple of 5 is 5.
So therefore since the formula holds when n=1, from what we proved above,
the formula will also hold when n=1+1=2.
So therefore since the formula holds when n=2, from what we proved above,
the formula will also hold when n=+1=3.
So therefore since the formula holds when n=3, from what we proved above,
the formula will also hold when n=3+1=4.
etc., etc., etc.,
This never stops, so the formula holds for all integers n.
[Many books teach you to do the second part first and the first part second,
so you can reverse them if you like.]
Edwin
Indeed it works for n=5 because the first positive multiple of 5 is 5.
So therefore since the formula holds when n=1, from what we proved above,
the formula will also hold when n=1+1=2.
So therefore since the formula holds when n=2, from what we proved above,
the formula will also hold when n=+1=3.
So therefore since the formula holds when n=3, from what we proved above,
the formula will also hold when n=3+1=4.
etc., etc., etc.,
This never stops, so the formula holds for all integers n.
[Many books teach you to do the second part first and the first part second,
so you can reverse them if you like.]
Edwin