Question 929314: Compute P(X) using the binomial probability formula. Then determine whether the normal distribution can be used to estimate this probability. If so, approximate P(X) using the normal distribution and compare the result with the exact probability.
n=58
p=0.3
x=12
ANSWER A, B, AND C BELOW.
a) For n=58, p= 0.3, and x=12, use the binomial probability formula to find P(X).
b) Approxiamte P(x) using the normal distribution. Use a standard distribution table.
c)By how much to the probabilities differ?
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website! n=58, p= 0.3, q = .7
........
a) P(x=12) = 58C12(.3)^12(.7)^46 0r P(x=12) = binompdf(58, .3,12) = .0355
b) normal distribution can be used to estimate this probability: both np and nq ≥ 5
.........
Using a Casio fx-115 ES plus
mean = .3•58 = 17.4, s = 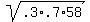 = 3.49 = 3.49
P(x = 12) = normalpdf(12, 3.49, 17.4) = .0345
....
c) .0355 - .0345 = .0010, the amount the probabilities differ
|
|
|